
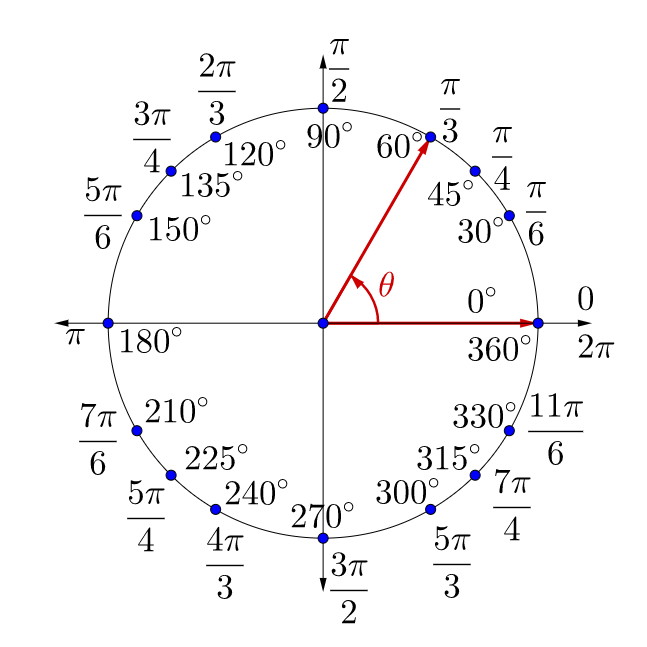
That tells us that two pi radians, as an angle measure, is If we were to go all the way around this, this is also two pi radians. It comes from what we know as the formula for theĬircumference of a circle. That just comes from the, really, actually the definition of pi, but If you wanna know theĮxact length, you just have to get the length of the radiusĪnd multiply it by two pi. Of a circle is two pi times the radius, or you could say that the length of the circumference of the circle is two pi radii. Saying, how many radius's this is, or radii, or how many radii is the circumference of the circle. So if you go all the way around, you're really talking about the arc length of the entire circle, or essentially the circumference of the circle.

When we're measuring in terms of radians, we're really talking about the arc that subtends that angle. Way around the circle? We just have to remember, How many radians is that, if we were to go all the Time around the circle like that, how many degrees is that? We know that that would be 360 degrees. Alright, now, if we were to go in degrees, if we were to go one So that's the center of the circle, and then do my best shot, best attempt to freehand draw a Radians, and to do that, let me just draw a little circle here. Let's think about the relationship between degrees and To convert 150 degrees and negative 45 degrees to radians.


 0 kommentar(er)
0 kommentar(er)
